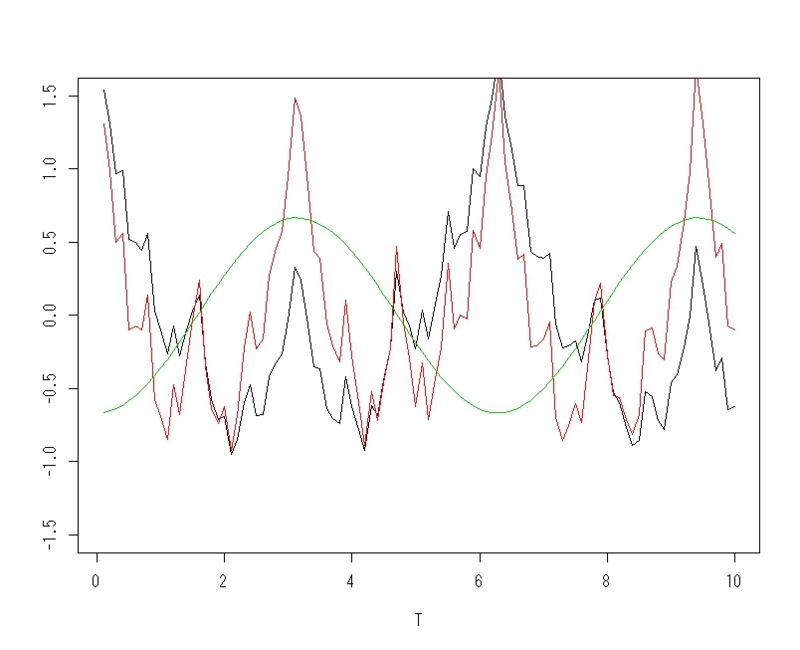
　1.2 複雑な変化 - 魚料理好きの日記

周期関数の振幅をα倍、周期数をβ倍していき、その級数和をとると、ワイエルシュトラス関数とよばれ、
$x(t)=\sum^{N}_{j=0} \alpha^{j+1} \cos (\beta ^j t) , | \alpha | < 1$
と表せる。
ホワイトノイズはこれで表現できる。
$x( \beta t)= \alpha^{-1} x(t)- \cos(t)$
で、時間軸と関数値軸を異なるスケール変換しているので、自己アフィン相似性とよぶ。

s<-0.1
T<-1:100*s
N<-50
alpha<-2/3
beta<-2
x<-c()
ax<-c()
#x(t)の計算
for(i in 1:length(T)){f<-function(x,i){(alpha^(x+1))*cos((beta^(x))*i*s)}
                      x[i]<-sum(f(0:N,i))
                      }
plot(T,x,type="l",ylim=c(-1.5,1.5),ylab=(""))
#αx(βt)の計算
for(i in 1:length(T)){f<-function(x,i){(alpha^(x+1))*cos((beta^(x+1))*i*s)}
                      ax[i]<-sum(f(0:N,i))
                      }
par(new=TRUE)
plot(T,ax,type="l",col=2,ylim=c(-1.5,1.5),ylab=(""))
par(new=TRUE)
#２関数の差
plot(T,(alpha*ax-x),type="l",col=3,ylim=c(-1.5,1.5),ylab=(""))

べき関数 $x(t)=A(t)t^{\gamma}$ が $\alpha x ( \beta t)=x(t)$ を満たすときの条件は
$\alpha \beta ^{\gamma}=1 , A(\beta t)=A(t)$ なので
$x(t)=t^{\frac{\log 1/\alpha }{\log \beta}} \sum^{\infty}_{j=-\infty} A_j \exp (i 2 \pi \frac{\log t}{\log \beta} j )$ と表される。
グラフとしてのフラクタル次元Dは
$D=2-\frac{\log ( 1/\alpha )}{\log \beta}$
と表される。
$H=2-D$ はハースト数とよばれる。

べき関数を $x(t)=\sum^{\infty}_{j=-\infty} A_j t^{H_j}$ と書き直すと
べき指数 $H_j=\frac{\log 1/\alpha }{\log \beta}-\frac{i2\pi j}{\log \beta}$ は複素数で、人の肺・地震・金融に応用されるらしい。