3章　Fitness landscape and Sequence spaces

3.1 sequence space
長さLのsequenceがあったときに、有り得るsequenceは $4^{L}$ 通り。(A,T,C,G)
このL次元空間をsequence spaceとする。
これを2進数(0,1)で考えると、L次元の超立方体の格子点があり得る組み合わせとなる。
各格子点の距離はマンハッタン距離で考えられる。

3.2 Fitness landscape
Fitness landscapeはsequence space状の格子点に対し、数値(reproduction rate)を与えたもの。
各格子点の評価みたいなもの。

3.3 the equasispecies equation
2進数でのsequence spaceを考え、それぞれの格子点を10進数に変換すると0から $2^{L}-1$ まで1対1で配列番号として与える。
i番目の配列に対して、 $x_{i},f_{i},Q_{ji}$ をそれぞれiの割合、適応度、配列jからiへの変異行列とすると、
$\dot{x_{i}}=\sum^{n}_{j=1}x_{j}f_{j}Q_{ji}-\phi x_{i}$
ただし、 $\phi = \sum^{n}_{i=1} f_{i} x_{i}$
をequasispecies equationという。
Qが単位行列、つまり変異が起きないなら最も高い $f_{i}$ 　をもつ配列iが生き残る。
Qが単位行列でないなら、単体内のある点 $x^{\ast}$ 　に収束する。このときφは必ずしも最大値とはならない。
しかし、総個体数はφの指数関数で増加する。

#試行回数
t<-30
#変異しうる配列数
n<-10
#遺伝子iを持つ個体の割合ベクトル
x<-runif(n)
x<-x/sum(x)
#遺伝子iを持つ個体のfittnessベクトル
f<-runif(n)
#mutation matrix
Q<-matrix(runif(n*n),n,n)
q<-apply(Q,1,sum)
Q<-Q/q
#average fittness
phi<-x%*%f

a<-matrix(0,n,t+1)
a[,1]<-x
for(i in 1:t){
dx<-(x*f)%*%Q-phi%*%x
x<-x+dx
a[,i+1]<-x
phi<-x%*%f
}
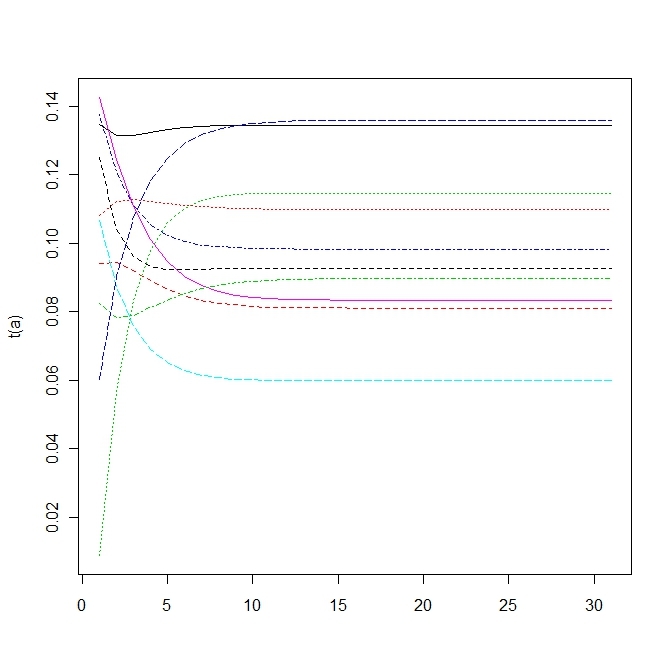
matplot(t(a),type="l")

3.4 a mutation matrix for point mutations
配列i,jのハミング距離を $h_{ij}$ として、点変異の入る確率をuとすると
変異行列Qの各成分(iからjと変異する確率)は
$q_{ij}=u^{h_{ij}}(1-u)^{L-h_{ij}}$

3.5 a adaptation is localization in sequence space
変異する確率が高すぎると適応していた個体(fittnessの値が高い)の割合がいまいち増えない。

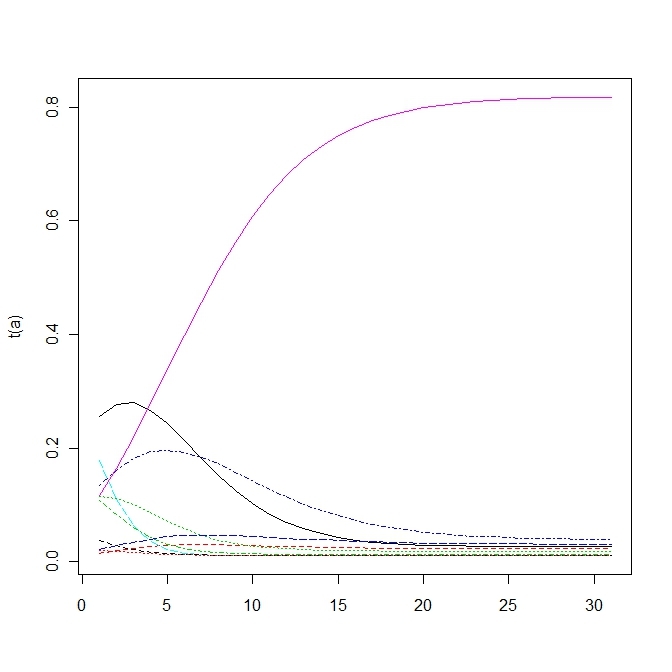
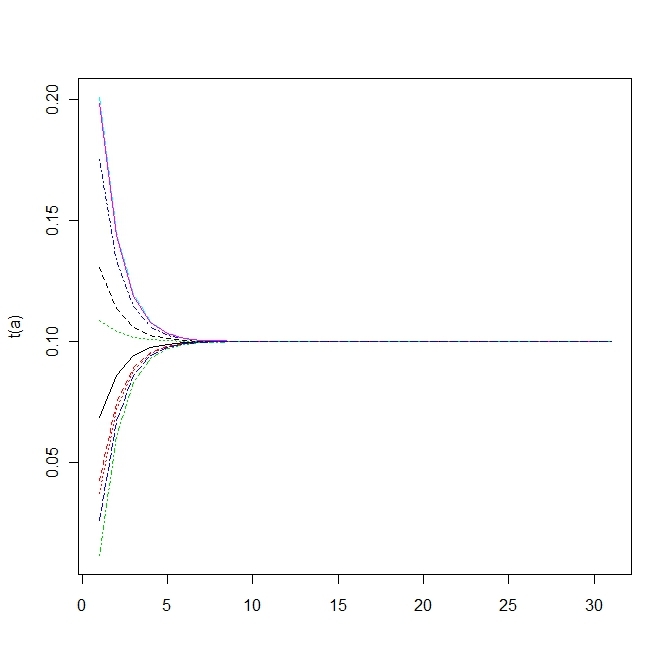
上の方は変異確率を1/100にしたもので、下の方は1/10にしたもので、上だともっとも高いfittnessをもつものに収束する。
単純なモデルでこの変異の閾値を計算すると $u<\frac{1}{L}$ 　という条件が求められる。
つまり $uL<1$ で、RNAウイルス、大腸菌、酵母菌、マウス、人などでuLの実測値が1より低いという論文が出ているらしい(Drake(1991,1998))。
一方で、QβウイルスとVZVウイルスは1よりはるかに大きく、その理由は不明。

3.6 selection of the quasispecies
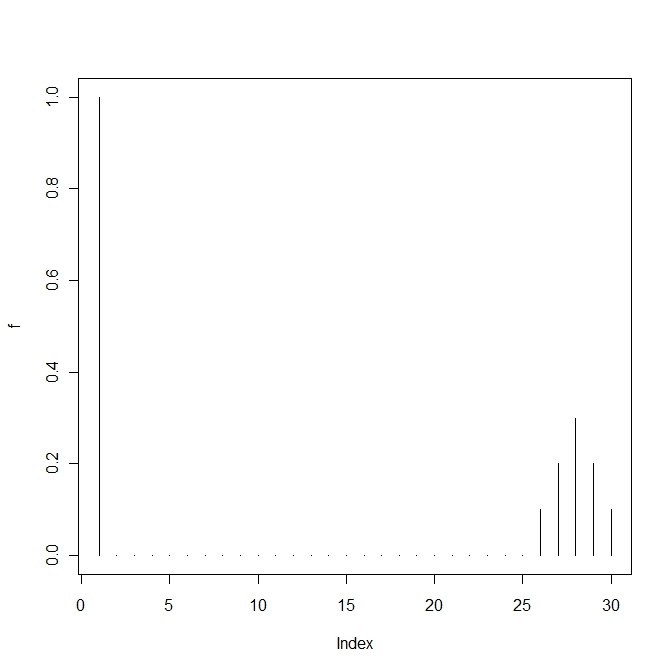
2峰性のfittness landscapeをもち、1つは高いが狭く、1つは高くはないが幅広とする。
このとき、変異の割合によって生き残りが変わってくる。
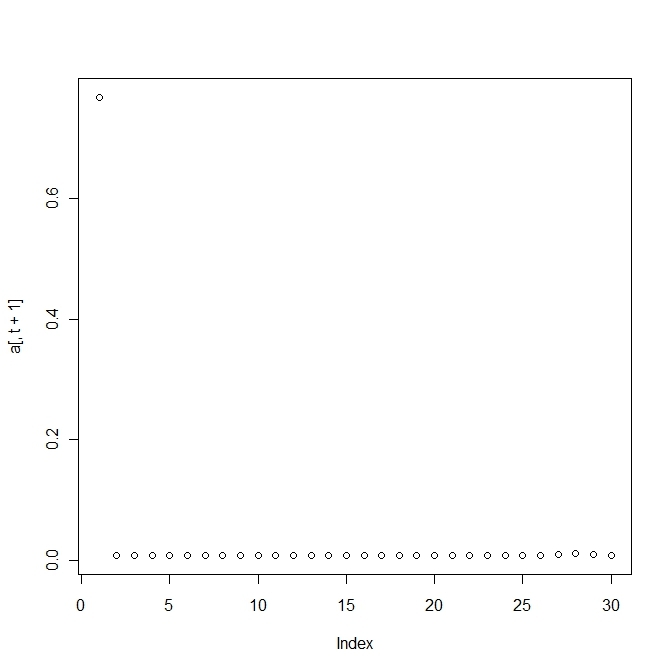
変異の割合が高すぎればすべての種が生き残り、低すぎると最も高いものに収束する。
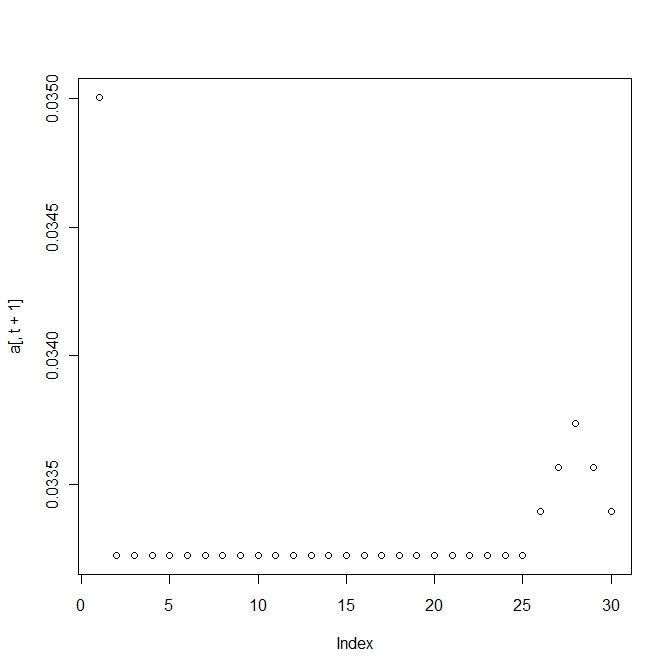
その中間であれば、2つのピークをもつ種が生き残る。

#試行回数
t<-100
#変異しうる配列数
n<-30
#遺伝子iを持つ個体の割合ベクトル
x<-runif(n)
x<-x/sum(x)
#遺伝子iを持つ個体のfittnessベクトル
f<-c(1,rep(0,n-1))+c(rep(0,n-5),0.1,0.2,0.3,0.2,0.1)
#mutationの割合を調整するパラメーター
h<-100
#mutation matrix
Q<-matrix(1,n,n)+h*diag(n)
q<-apply(Q,1,sum)
Q<-Q/q
#average fittness
phi<-x%*%f

a<-matrix(0,n,t+1)
a[,1]<-x
for(i in 1:t){
dx<-(x*f)%*%Q-phi%*%x
x<-x+dx
a[,i+1]<-x
phi<-x%*%f
}
plot(a[,t+1])